Page 31 - Appplied Mathematics for the Petroleum and Other Industries, 5th Edition

208 ADVANCED MATH CONCEPTS

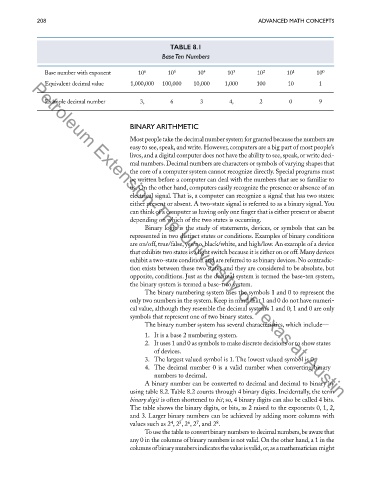
TABLE 8.1
Base Ten Numbers

1
3
5
6
2
Base number with exponent 10 10 10 10 10 10 10 0
4
Equivalent decimal value 1,000,000 100,000 10,000 1,000 100 10 1
Example decimal number 3, 6 3 4, 2 0 9

BINARY ARITHMETIC
Most people take the decimal number system for granted because the numbers are
easy to see, speak, and write. However, computers are a big part of most people’s
lives, and a digital computer does not have the ability to see, speak, or write deci-
mal numbers. Decimal numbers are characters or symbols of varying shapes that
the core of a computer system cannot recognize directly. Special programs must
be written before a computer can deal with the numbers that are so familiar to
us. On the other hand, computers easily recognize the presence or absence of an
electrical signal. That is, a computer can recognize a signal that has two states:
either present or absent. A two-state signal is referred to as a binary signal. You
can think of a computer as having only one finger that is either present or absent
depending on which of the two states is occurring.
Binary logic is the study of statements, devices, or symbols that can be
represented in two distinct states or conditions. Examples of binary conditions
are on/off, true/false, yes/no, black/white, and high/low. An example of a device
that exhibits two states is a light switch because it is either on or off. Many devices
exhibit a two-state condition and are referred to as binary devices. No contradic-
tion exists between these two states and they are considered to be absolute, but
opposite, conditions. Just as the decimal system is termed the base-ten system,
the binary system is termed a base-two system.
The binary numbering system uses the symbols 1 and 0 to represent the
only two numbers in the system. Keep in mind that 1 and 0 do not have numeri-
cal value, although they resemble the decimal system’s 1 and 0; 1 and 0 are only
symbols that represent one of two binary states.
The binary number system has several characteristics, which include—
1. It is a base 2 numbering system.
2. It uses 1 and 0 as symbols to make discrete decisions or to show states
of devices.
3. The largest valued symbol is 1. The lowest valued symbol is 0.
4. The decimal number 0 is a valid number when converting binary
numbers to decimal.
A binary number can be converted to decimal and decimal to binary by
Petroleum Extension-The University of Texas at Austin
using table 8.2. Table 8.2 counts through 4 binary digits. Incidentally, the term
binary digit is often shortened to bit; so, 4 binary digits can also be called 4 bits.
The table shows the binary digits, or bits, as 2 raised to the exponents 0, 1, 2,
and 3. Larger binary numbers can be achieved by adding more columns with
7
values such as 2 , 2 , 2 , 2 , and 2 .
8
4
5
6
To use the table to convert binary numbers to decimal numbers, be aware that
any 0 in the columns of binary numbers is not valid. On the other hand, a 1 in the
columns of binary numbers indicates the value is valid, or, as a mathematician might